Experimental design guide
The relevance of your image analysis results will depend on the design of your experiment and the use of a statistical model that takes into account the structure of the data. Experimental design must be carefully considered before commencing any practical work. The purpose of this guide is to:
- provide some fundamental design notions.
- clarify the design-related terminology used in Melanie.
- enumerate the designs that are specifically supported by Melanie.
- explain how to proceed for the analysis of a design that is not specifically supported.
References
We recommend the references below for a more in-depth review of experimental design applied to proteomic analyses.
- Cairns, D. A. (2011). Statistical issues in quality control of proteomic analyses: good experimental design and planning. Proteomics, 11(6), 1037-1048. http://www.ncbi.nlm.nih.gov/pubmed/21298792
- Chich, J.-F., David, O., Villers, F., Schaeffer, B., Lutomski, D., & Huet, S. (2007). Statistics for proteomics: Experimental design and 2-DE differential analysis. Journal of Chromatography B, 849(1–2), 261-272. https://doi.org/10.1016/j.jchromb.2006.09.033
- Dautel, F., Kalkhof, S., Trump, S., Lehmann, I., Beyer, A., & Von Bergen, M. (2011). Large-scale 2-D DIGE studies – Guidelines to overcome pitfalls and challenges along the experimental procedure. Journal of Integrated OMICS, 1. https://doi.org/10.5584/jiomics.v1i1.50
- Karp, N. A., & Lilley, K. S. (2007). Design and analysis issues in quantitative proteomics studies. Proteomics, 7(Suppl 1), 42-50. https://doi.org/10.1002/pmic.200700683
- Oberg, A. L., & Vitek, O. (2009). Statistical design of quantitative mass spectrometry-based proteomic experiments. Journal of Proteome Research, 8(5), 2144-2156. https://pubs.acs.org/doi/10.1021/pr8010099
Experimentation
An experiment deliberately imposes a treatment on a group of objects or subjects in the interest of observing the response.
Treatments are administered to experimental units. The experimental unit is the smallest sub-division of the experimental material such that two different experimental units might receive different treatments (or samples applied to them). In an investigation using 2-D PAGE, it is the gel on which the sample is run. In a 2-D DIGE experiment, it is the combination of the gel and dye.
Treatments are administered to experimental units by level, where level implies amount or value. For example, if the experimental units were given Drug A, Drug B or Drug C, those would be three levels of the treatment.
A factor of an experiment is a controlled independent variable; a variable whose levels are set by the experimenter. A factor is a general type or category of treatments. Different treatments constitute different levels of a factor. In the example above, Drug A, Drug B and Drug C constitute the three levels of the factor ‘Medication’.
Experimental design
Experimental design is the process of:
- Formulating a scientific hypothesis, and the relevant statistical hypothesis.
- Determining the treatment levels (independent variables) to be manipulated, the measurement to be recorded (dependent variable), and the extraneous conditions (nuisance variables) that must be controlled.
- Specifying the number of experimental units required and the population from which they will be sampled.
- Specifying the randomization procedure for assigning the experimental units to the treatment levels.
- Determining the statistical analysis that will be performed.
The primary goal of an experimental design is to avoid bias, that is, systematic errors in statistical inferences about the populations. Second, it ensures that the experiment is efficient, that is, it minimizes the random variation for a given amount of cost.
The three fundamental principles in the design of an experiment are: randomization, blocking and replication.
Randomization
Randomization refers to the order in which the trials of an experiment are performed. A randomized sequence helps eliminate effects of unknown or uncontrolled variables.
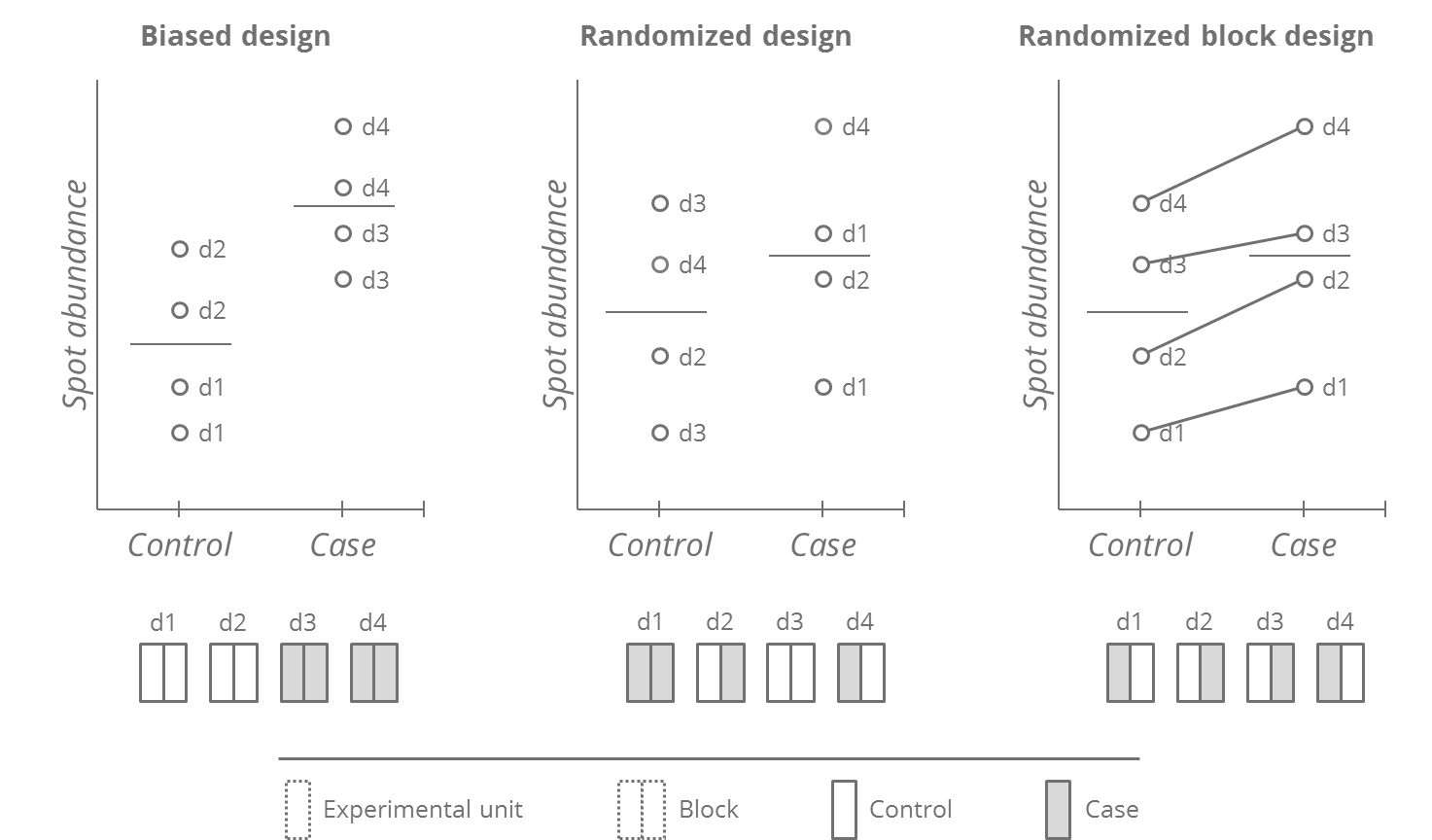
As an example, imagine the Biased design in the figure below. It seems that the Controls have lower spot volumes than the Cases. But this effect might be due to the order in which the gels were run (e.g. differences in lab temperature on different days, potentially leading to proteolysis of certain proteins). Randomization ensures that biases caused by aberrant and unknown experimental artifacts cannot affect the conclusions inferred from measurements, by allowing each combination of experimental unit and sample applied to it, an equal chance of being affected by these artifacts.
Blocking
Blocking helps reduce the bias and variance due to known sources of experimental variation (nuisance variable).
The Randomized design in the above figure has two drawbacks. Randomization can potentially produce unequal allocations (assigning more Cases toward days 1 and 2), and inflate the variability within each group by a combination of the biological and of the day-to-day variation. This may make it difficult to detect the true differences between groups. Randomized block designs enforce a balanced allocation of treatments between blocks (in the example, a block is a day). They do this by first dividing the experimental subjects into homogeneous blocks before they are randomly assigned to a treatment group. The use of an appropriate statistical model can further provide block-corrected estimates of the difference between Cases and Controls. Indeed, the figure shows that despite large within-block variation, case-control differences are consistent.
A particular example of blocking often used in 3-dye DIGE experiments is dye-swap, where it is recommended to evenly distribute the treatments between the Cy3 and Cy5 dyes.
Note that a paired design is a special case of blocking, in which the blocks are individual subjects. For example, a study that measures protein expression before and after taking a drug would form blocks in which each subject would be within his or her own block and would base the analysis on the difference in each subject’s spot abundances before and after treatment.
Replication
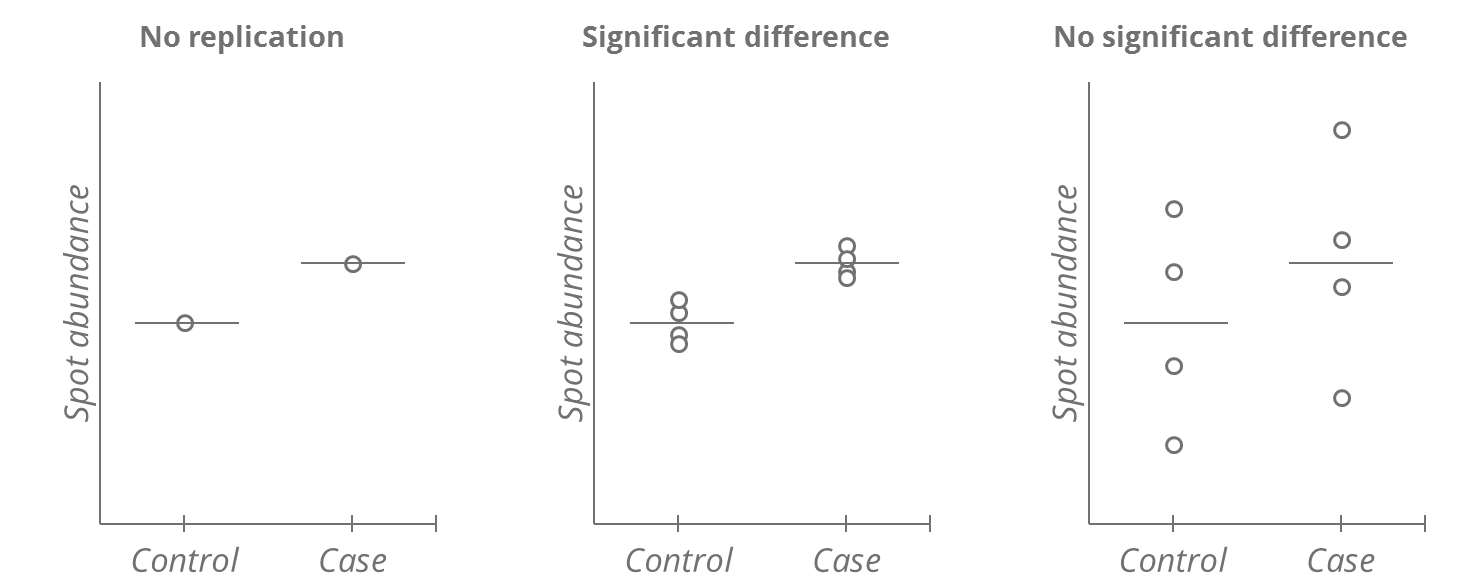
An experiment contains replication if the same treatment is applied independently to two or more experimental units. It allows one to assess whether the observed difference in a measurement is likely to occur by random chance.
In the figure below, without replication, it is impossible to say whether the observed difference between Controls and Cases represents the true difference between the populations, or if it is an artifact of selecting these specific individuals, or of the measurement error. Replication allows to distinguish these situations. Increasing the number of replications also results in a more precise inference regarding differences between treatment groups. A larger number of replicates may allow to demonstrate a treatment effect, despite large variation.
Factors and factor relations
Fixed and random factors
Fixed factors (or fixed effects treatment factors) have levels that are assumed to be fixed (reproducible). Inference is restricted to those levels of the factor that were included in the study. The parameters of interest are the treatment effects.
Random factors (or random effects treatment factors) have levels that are assumed to represent a random sample of the potential levels within a well defined population. Inference is directed to the population. The parameters of interest are the variance components.
Random effects factors are rarely used in 2D gel electrophoresis experiments, and Melanie does not support them. The software assumes that all factors studied are fixed effects treatment factors.
Crossed and nested designs
When there is only one factor in a design, there is no need to worry about crossing and nesting. But when there are at least two factors, you need to understand whether they are crossed or nested, because it will affect the analyses you can and should conduct.
Two factors are crossed when each level of one factor occurs in combination with each level of the other factor. In other words, there is at least one observation in every combination of categories for the two factors.
A factor is nested within another factor when each category of the first factor co-occurs with only one category of the other. In other words, an observation has to be within one category of Factor 2 in order to have a specific category of Factor 1. All combinations of categories are not represented.
If two factors are crossed, you can calculate an interaction. If they are nested, you cannot because you do not have every combination of one factor along with every combination of the other.
Supported designs in Melanie
A carefully designed experiment can still be wasted if subsequent statistical analysis does not take into account the structure of the data. If, in the illustrated randomized block design above, one ignores the paired allocation of experimental units within a day and compares average spot abundances in each group, one does not improve the ability to detect the true differences.
On the other hand, the number of possible designs, and the applicable statistical models, are virtually unlimited. It is not possible or even sensible for Melanie to attempt supporting all statistical test models. Dedicated statistical packages exist for that.
Therefore, Melanie only provides specific statistical support for a few common one- and two-factor experiments that are described here. For experiments that have been designed to study three or more primary factors, or that integrate more advanced design notions, you can still align and detect your images, filter, edit and normalize spots, and use some of the statistical tools for exploration. However, for such experiments, we strongly advice you to export your data for appropriate statistical analysis with third party software, under the guidance of a statistician.
One-factor experiment
- Single factor A (Fixed) with two or more treatment levels.
- Each treatment level contains a number of replicates, i.e. images. The number of replicates in the different treatments need not be balanced.
- This randomized design will be analyzed with ordinary one-way ANOVA.
One-factor experiment with subjects
- Single factor A (Fixed) with two or more treatment levels.
- For each subject in the experiment, all treatment levels of Factor A are applied. For instance, a sample was taken from each subject before, during and after a treatment. No missing values are allowed; for every subject included, there must be a value for each factor A level.
- This paired design will be analyzed with repeated measures one-way ANOVA.
One-factor experiment with blocking
- Single factor A (Fixed) with two or more treatment levels.
- The design includes a blocking factor T (Random) that aims to reduce bias and variance for a known source of experimental variation. For instance, to account for expected variance due to different lab technicians running the gels, a block can be created for each technician, and the treatments be randomly assigned within each block.
- This randomized block design will be analyzed with repeated measures one-way ANOVA.
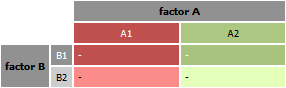
Two-factor experiment
- A factor A (Fixed) with two or more treatment levels is crossed with a factor B (Fixed), also with two or more treatment levels.
- The experiment can be replicated. The number of replicates need to be balanced across all treatment combinations.
- This complete randomized design will be analyzed with ordinary two-way ANOVA.
Two-factors with subjects
- A factor A (Fixed) with two or more treatment levels is crossed with a factor B (Fixed), also with two or more treatment levels.
- An additional subject factor S is crossed with factor A and nested within factor B. In this design, factor A is also called a within-subject factor, while factor B is a between-subject factor.
- This paired design will be analyzed with repeated-measures two-way ANOVA.
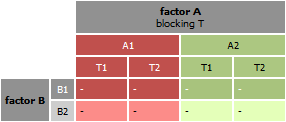
Two-factors with blocking
- A factor A (Fixed) with two or more treatment levels is crossed with a factor B (Fixed), also with two or more treatment levels.
- The design includes a blocking factor T (Random) that aims to reduce bias and variance for a known source of experimental variation. For instance, to account for expected variance due to different lab technicians running the gels, a block can be created for each technician, and the treatments be randomly assigned within each block.
- This randomized block design will be analyzed with repeated-measures two-way ANOVA.